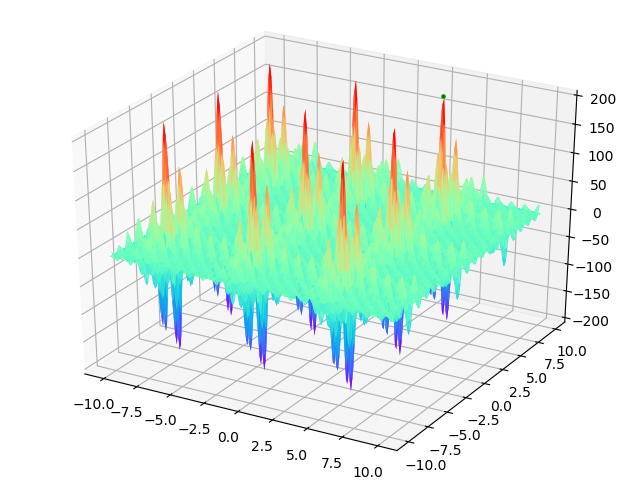
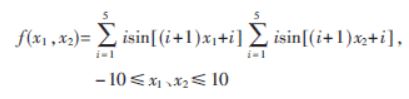特点
- 两个自变量
- 范围[-10,10]
- 周期函数
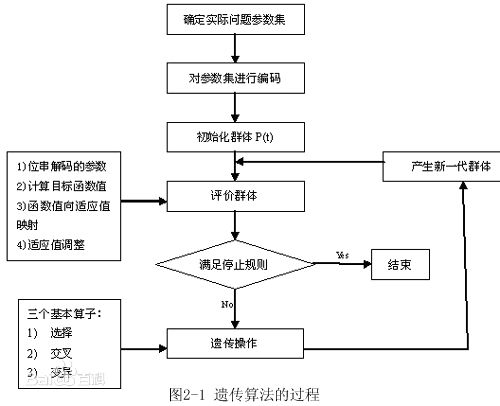
遗传算法(Genetic Algorithm)是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法。(百度百科)
进化学说的一些观点
- 进化以中群为单位
- 自然选择决定进化的方向
- 变异具有不确定性
- 变异为进化提供原材料
遗传算法需要模拟进化中的几个过程
- 可能发生交叉互换。
- 可能产生基因突变。
- 每个个体具有不同的个体差异,产生子代的概率不同,模拟自然选择。
以上几点很重要,前两点产生新的类型,虽然不定向变异,但有机会产生更优的答案。而第三点,隐含了启发式信息。结合进化学说中的观点,可知,应选择一定数量的个体来模拟进化(种群为单位)。
遗传算法解决问题的一般思路
语言:python版本:v3.6.0
库:math copy numpy matplotlib
主要函数:
- 编码函数Encode()
- 解码函数Decode()
- 变异函数getChange()
- 交叉函数getSwap()
- 产生子代getNextGen()
编码方式分类
- 二进制编码
- 格雷码编码
- 浮点数编码
- 排列编码
本程序采用二进制编码,将两个自变量的取值精确到0.01(1/1024),用22位二进制编码变量。编码基因型使得交叉和变异变得容易模拟,只需模拟某一位的编码的改变或互换即可模拟表现型的改变。
子代个体产生方法
- 轮盘赌选择法
- 随即遍历抽样
- 锦标赛算法
适应度评估是通过函数的值的大小来评估,然而此函数的值中有负数的存在。轮盘赌算法不适用,本程序采用将适应度统一增加225。当然也有其他的解决思路,可以采用锦标赛方法产生后续个体,这种方法类似于有放回的摸球方法。
结果分析
- 量化导致的误差,因为,量化精度为1/1024。分析此函数的连续性和周期性可得出,取得最值的点的位置相对于量化点的位置不一定完全一样,所以导致程序求的不同峰值的最优解不相同。
- 进化压力偏大可能导致种群进化到某一个较低的极值点位置而不易变异到更高的最值处。所以应控制进化压力的大小在一个合适的范围。
总结
使用遗传算法求解函数极值的方法还是比较得心应手的。通过本次作业,了解到算法对于程序的重要意义,也发现自己本身所欠缺的正是这种算法的积累。
在编程中学到的一些python的知识点现总结如下
- numpy中的数组与python中的列表不是一种数据结构
- 深复制与浅复制,python直接将该数组中的值赋值添加到其他列表属于浅复制。修改其中一个,另一个仍会修改。
- matplotlib库,数据可视化,可轻松画出美观的图像,是便于理解数据规律的好工具。