Conversation
|
Derived a second derivative formula for NURBS. I suspect there's some way to do better than this. I don't know. Octave's implementation has bernstein polynomials or something, but that's for de casteljau's algorithm (b-splines), not de boor's (nurbs)? Or something. Here's the last few lines of a derivation for the second derivative of nurbs that requires passing a bit of extra information from the second-to-last level to the last level of de boor's algorithm. In particular, the weights, the derivative of the weights (which is real simple since they're just b-splines), and the derivative and the function value. Which basically just means some extra bookkeeping. It's a bit annoying, but not really difficult. |
|
Oh fun. Note that if weights are 1, the first term goes away, which affirms the fact that it's a correction to the simple/obvious form (the second term) that works for b-splines. |
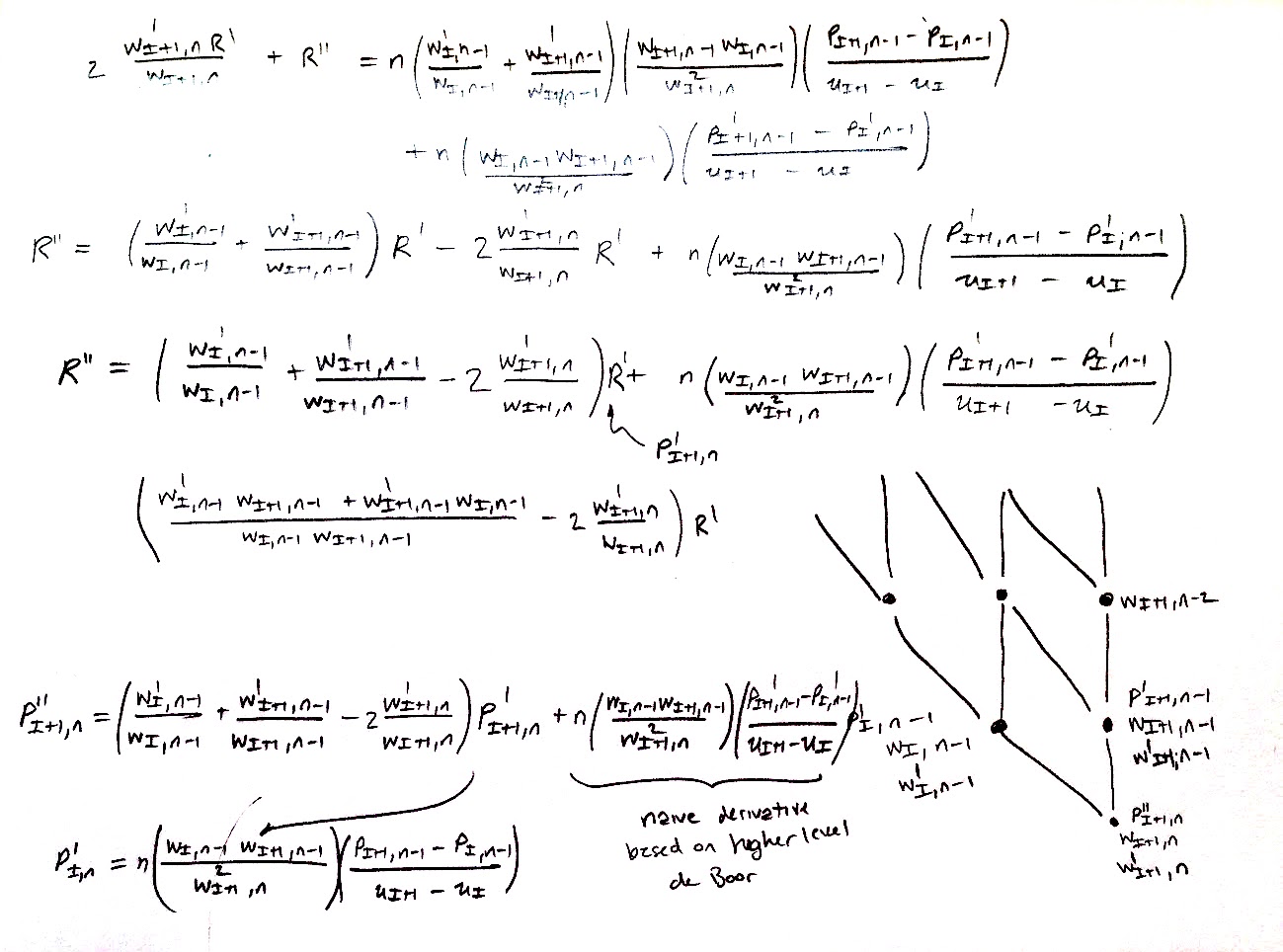
A working branch for higher order derivatives. Still haven't figured out the math, but it's in progress. This branch currently just adds finite difference comparisons through fourth order, which should be tested anyway. Higher order derivatives works fine with knots, but give the incorrect answer if you turn on weights.