- 알고리즘
- 전체 코드
- 성능 분석 및 결과
- 회귀(regression)
모의 담금질(Simulated Annealing) 기법은 높은 온도에서 액체 상태인 물질이 온도가 점차 낮아지면서 결정체로 변하는 과정을 모방한 해 탐색 알고리즘이다 .온도가 점점 낮아지면 분자의 움직임이 점점 줄어들어 결정체가 되는데, 해 탐색 과정도 이와 유사하게 점점 더 규칙적인 방식으로 이루어진다.이러한 방식으로 해를 탐색하려면, 후보해에 대해 이웃하는 해 (이웃해)를 정의하여야 한다.
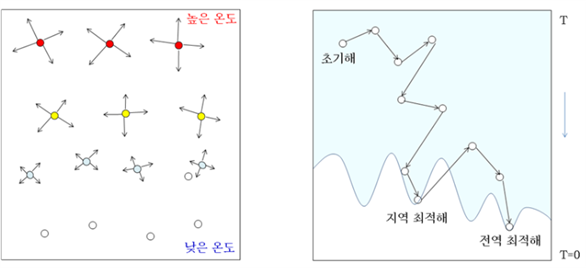
높은 T에서의 초기탐색은 최솟값을 찾는데도 불구하고 확률 개념을 도입하여 현재 해의 이웃해 중에서 현재 해보다 나쁜해로 이동하는 자유로움을 보인다. 그러나 T가 낮아지면서 점차 탐색은 아래방향으로 향하는데 이는 T가 낮아질수록 위방으로 이동하는 확률이 점차 작아진다는 것이다.
public class Main {
public static void main(String[] args) {
SimulatedAnnealing sa = new SimulatedAnnealing(1, 0.98, 100);
sa.solve(new Problem() {
@Override
public double fit(double x) {
return -0.1*x*x*x*x -x*x +0.2*x + 5;
}
@Override
public boolean isNeighborBetter(double f0, double f1) {
return f1 > f0;
}
}, 0, 31);
System.out.println(sa.hist);
}
}함수를 -0.1x^4-x^2+0.2x+5로 정의하였고, 초기온도는 1을 선택했고, a(냉각률)은 a는 0.98부터 값을 바꿔 보았고, niter 100으로 설정하였다.
import java.util.ArrayList;
import java.util.Random;
public class SimulatedAnnealing {
private double t; // 초기온도
private double a; // 냉각비율
private int niter; // 종료조건(반복 횟수)
public ArrayList<Double> hist;
public SimulatedAnnealing(double t, double a, int niter) {
this.t = t;
this.a = a;
this.niter = niter;
hist = new ArrayList<>();
}
public double solve(Problem p, double lower, double upper) {
Random r = new Random();
double x0 = r.nextDouble() * (upper - lower) + lower; // 초기후보해
double f0 = p.fit(x0); // 초기후보해의 적합도
hist.add(f0);
for(int i=0; i<niter; i++) { // REPEAT
int kt = (int) Math.round(t * 20);
for(int j=0; j<kt; j++) {
double x1 = r.nextDouble() * (upper - lower) + lower; // 이웃해 (lower~upper)
double f1 = p.fit(x1);
if(p.isNeighborBetter(f0, f1)) { // 이웃해가 초기후보해 보다 나을경우
x0 = x1; //후보해를 이웃해로 바꿈
f0 = f1;
hist.add(f0);
} else { // 기존해가 이웃해보다 더 나을 경우
double d = f1 - f0;
double p0 = 0.0001;
if(r.nextDouble() < p0) { //기존해가 이웃해보다 나아도 일정 확률(p0)로 바꿈
x0 = x1;
f0 = f1;
hist.add(f0);
}
}
}
t *= a; //a는 냉각률(일반적으로 0.99에 가까운 수를 선택하여, T가 천천히 감소되도록 조절한다.)
}
return x0;
}
}초기 후보해와 이웃해를 각각 랜덤함수로 받고 isNeighborBetter함수로 더 나은 함수를 선택 하는데 만약 이웃해가 초기 후보해보다 좋다면 후보해를 이웃해로 바꾸고, 기존해가 이웃해보다 더 낫더라도 일정 확률로 바꿀 수 있다.
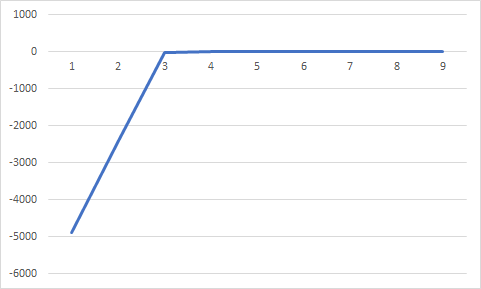
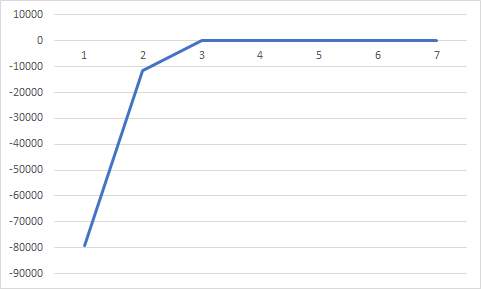
(t=1, a=0.98, niter=100, p0=0.0001)
p0값이 작아서 성능이 너무 잘나왔다. p0값을 0.0001->0.001로 바꿔주면,
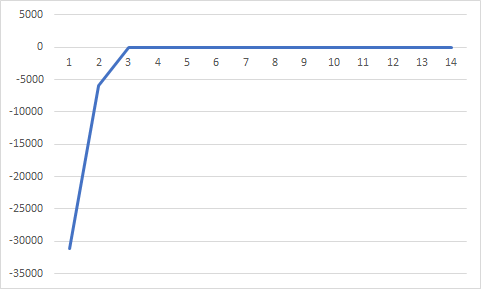
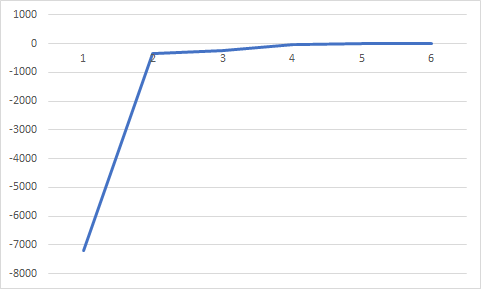
(t=1, a=0.98, niter=100, p0=0.001)
이와 같이 수행횟수가 약간 더 늘었다.
이번에는 p0값을 0.001->0.005로 바꾸어 주었다.
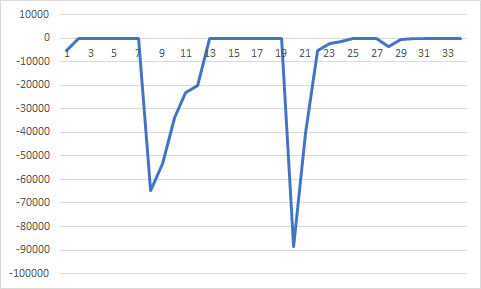
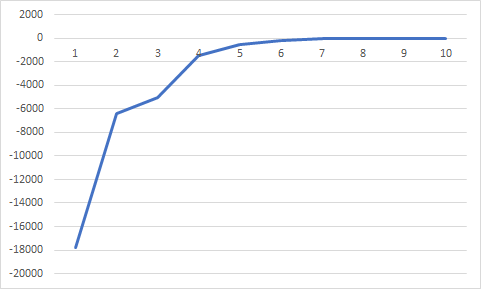
(t=1, a=0.98, niter=100, p0=0.005)
이와 같이 수행횟수도 늘어나고 위에서는 더 좋은 값으로만 가는 모습을 보였지만, p0가 커짐에 따라 현재해보다 나쁜 곳도 갔다오면서 최종적으로 최적점 값에 수렴하는 모습이다.
이번에는 마지막으로 p0를 좀 많이 크게 해보았다. p0=0.1
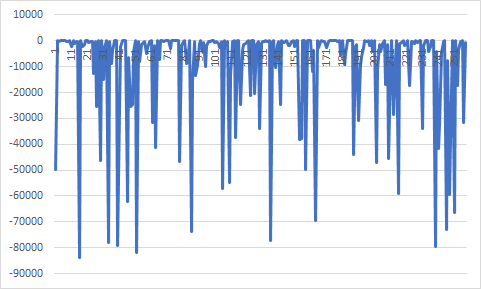
(t=1, a=0.98, niter=100, p0=0.1)
이와 같이 수행 횟수도 굉장히 맣이 늘어나고 결과값도 위에 있는 것들과는 달리 최적점과의 차이가 꽤 많이 났다. 이것으로 p0를 너무 크게 하면 최적점을 얻을 수 없다는 결론을 얻었다.
이번에는 a(냉각률)에 따른 변화를 관찰해 보겠다.
성능 관찰 맨 위의 그래프는 a=0.98의 그래프이다.
일반적으로 a는 0.99에 가까운 수로 선택하여, T가 천천히 감소되도록 한다.
a를 0.98->0.9로 변화시켜 보았다.
(t=1, a=0.9, niter=100, p0=0.0001)
위의 그래프와 큰 차이 없이 최적점에 수렴한다.
이번에는 a를 0.9->0.8로 변화시켜 보았다.
(t=1, a=0.8, niter=100, p0=0.0001)
약간의 횟수감소가 있고 큰 변화는 없어보인다.
이번에는 3차함수에 대해서도 최적점 값을 찾을 수 있는지 알아본다.
-2*x*x*x+4*x+2(t=1, a=0.98, niter=100, p0=0.0001)
이와 같이 최저점에 수렴한다.
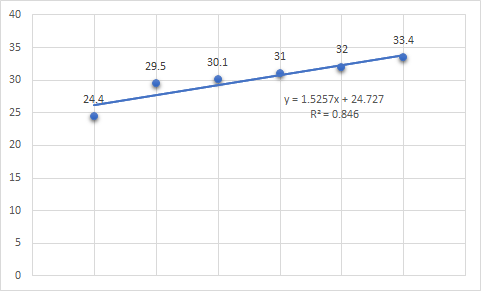
회귀는 독립변수(independent variable) 또는 예측인자(predictor)라 부르는 변수 X와 종속변수(dependent variable) 또는 예측량(predictand)이라 부르는 변수 Y의 관계를 함수식으로 설명하는 통계적 방법이다.
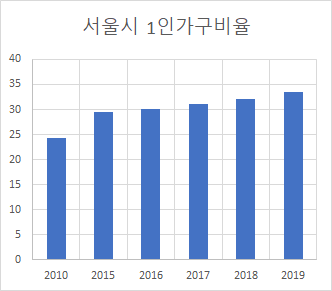
서울시 1인가구 비율이 매년 증가하고 있다.
여기서 독립변수 X를 년도로 뒀고 종속변수 Y를 서울시 1인가구 비율로 두었다.
이렇듯 매년 갈수록 서울시 1인가구 비율이 선형적으로 늘고 있다.
그래프를 보았을 때, 아마 앞으로도 쭉 늘 것처럼 보인다.